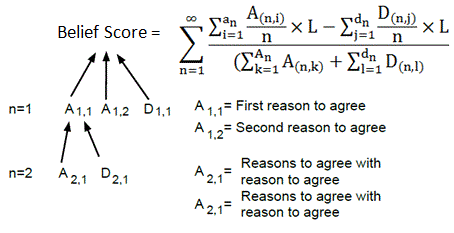Enriching Mathematical Learning Through the Practical Application of Algorithms

Dear Esteemed Mathematics Educators,

I am reaching out to you today with an exciting proposition - a unique opportunity to engage your students in the application of mathematical principles in an unconventional and meaningful way. It involves a novel algorithm designed to evaluate and promote ideas based on the strength of the reasoning and evidence provided.

Here is the formula we're discussing:

Conclusion Score (CS) = ∑ [(LS * RS_agree - LS * RS_disagree) * RIW]
+ ∑ [(LS * ES_agree - LS * ES_disagree) * EIW]
+ ∑ [(LS * IS_agree - LS * IS_disagree) * IIW]
+ ∑ [(LS * BS_agree - LS * BS_disagree) * BIW]
+ ∑ [(LS * IMS_agree - LS * IMS_disagree) * IMIW]
+ ∑ [(LS * MS_agree - LS * MS_disagree) * MIW]

More detailed information about these variables can be found on our websites: https://github.com/myklob/ideastockexchange and https://www.groupintel.org/.

In an era where discourse is increasingly digitized, this algorithm operates within a web-based forum. It allows users to submit reasons to agree or disagree with a belief, and encourages further discussion by allowing additional reasoning to be submitted for these primary arguments. The algorithm integrates these layers of discourse, forming an assessment of the belief's validity by counting and comparing reasons to agree and reasons to disagree.

Why introduce this into your mathematics curriculum?

1. Innovation: This algorithm provides a unique application of mathematical principles in an area traditionally untouched by such methods - the evaluation and promotion of ideas.

2. Engagement: By combining mathematics with discourse, debate, and real-world application, students can experience the practical and impactful side of their mathematical studies.

3. Idealism: This project aligns well with the idealistic nature of young minds. It enables students to contribute positively to global conversations, fostering a deeper connection to their learning.

4. Potential Impact: Just as Google's PageRank algorithm revolutionized the internet by ranking web pages based on their inbound links, our algorithm seeks to enhance discourse by assessing and promoting good ideas. This creates an informed and critical thinking internet community.

5. Towards a Smarter World: The development and use of such algorithms can contribute to a more informed, critical and intelligent world.

I encourage you to review this proposal and consider the immense potential it holds for enriching your curriculum and inspiring your students. I am eager to answer any questions or provide further information at your convenience.

Thank you for your time and consideration.

Best regards,
Mike

An open letter to Math teachers

I am writing you to ask for your assistance in promoting "good idea promoting algorithms" such as the following:

The above formula would work in an environment were you were able to submit reasons to agree or disagree with a belief, and then you could submit reasons to agree or disagree with those arguments. With this format it place you could count the reasons to agree and subtract the number of reasons to disagree, and then you could integrate the series of reasons to agree with reasons to agree.

You should use this equation because:

1. It is unique. I have never seen someone use an algorithm in an attempt to promote good ideas. Math can become more interesting when kids see the variety of ways it can be applied. 
2. Kids are idealistic, and often want to improve the world. Challenging them to try to come up with a good idea promoting algorithm can use this energy, to learn math.
3. This simple that counts the reasons to agree with a conclusion, could change the wold, similar to how Google's web-link counting algorithm changed the world. When lots of people link to a website, Google assumes that website is a good one. Then when that good website links to another website, Google assumes the 2nd website is a good one. Similarly when you submit good reasons to support an argument, a smart web forum would also give points to the conclusions that are built on that assumption. 
4. The more people make good idea promoting algorithms, the less stupid world we will live in.

Optimal Algorithm for Online Forums Utilizing Relational Databases for Debate

In an online forum that utilizes a relational database to track arguments either supporting or countering conclusions, and allows users to submit their beliefs as reasons to support other beliefs, the deployment of the following algorithm can prove highly advantageous:




Or with math:

The equation for the idea score can be represented as:

Basic Algorithm:

Conclusion Score (CS) is a weighted sum of different types of scores, each calculated as the difference between supporting and opposing elements for the given conclusion. It is represented as:

Conclusion Score (CS) = ∑ [(LS * RS_agree - LS * RS_disagree) * RIW]
+ ∑ [(LS * ES_agree - LS * ES_disagree) * EIW]
+ ∑ [(LS * IS_agree - LS * IS_disagree) * IIW]
+ ∑ [(LS * BS_agree - LS * BS_disagree) * BIW]
+ ∑ [(LS * IMS_agree - LS * IMS_disagree) * IMIW]
+ ∑ [(LS * MS_agree - LS * MS_disagree) * MIW]

Where:

• CS: Conclusion Score
• LS is the Linkage Score, representing the strength of the connection between an argument and the conclusion it supports.
• n represents the number of steps an argument is removed from an idea. For instance, a direct reason to agree or disagree is one step removed, whereas a reason to agree with a reason to agree is two steps removed.
• RS, ES, IS, BS, IMS, and MS are scores associated with reasons, evidence, investments, books, images, and movies respectively that support or counter the belief. Each score is associated with a weighting factor (RIW, EIW, IIW, BIW, IMIW, and MIW) to signify its importance.

The idea score is calculated by subtracting the sum of the argument scores multiplied by their respective linkage scores for the reasons to disagree from the sum of the argument scores multiplied by their respective linkage scores for the reasons to agree. This equation takes into account the relative strength and linkage of each argument in determining the overall idea score.

The equation for the linkage score can be represented as:

The linkage score is calculated by subtracting the sum of the sub argument scores that disagree from the sum of the sub argument scores that agree, and then dividing it by the total number of arguments. This value is then multiplied by 100% to express the result as a percentage. The linkage score represents the percentage of weighted scores that agree with the belief, indicating the strength of the agreement among the sub arguments in relation to the total number of arguments.

Unique Score (US) = [(Sum of scores agreeing that two statements are unique) - (Sum of scores disagreeing that two statements are unique)] / (Total argument scores) * 100

This score evaluates the uniqueness of two statements, normalizing it by the total argument scores. The score ranges from -100 to +100, where -100 indicates full agreement that two statements are not unique (or identical), and +100 indicates full agreement that two statements are indeed unique.