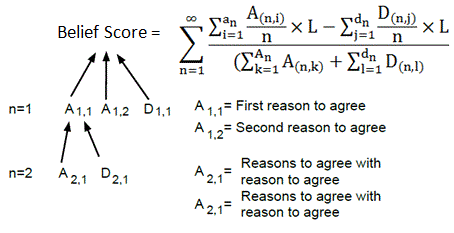Scoring Beliefs and Conclusions: An Algorithmic Approach for an Online Forum

This online forum employs a relational database to catalog reasons supporting or opposing various conclusions. It allows users to submit a belief as evidence to back another belief (Refer to Figure #1). According to Equation #1, a conclusion receives a score derived from the scores of its underpinning assumptions. Similarly, assumption scores are calculated based on their corresponding assumptions, until we reach verifiable data.

Basic Algorithm:

Conclusion Score (CS) is a weighted sum of different types of scores, each calculated as the difference between supporting and opposing elements for the given conclusion. It is represented as:

Conclusion Score (CS) = ∑ [(LS * RS_agree - LS * RS_disagree) * RIW]
+ ∑ [(LS * ES_agree - LS * ES_disagree) * EIW]
+ ∑ [(LS * IS_agree - LS * IS_disagree) * IIW]
+ ∑ [(LS * BS_agree - LS * BS_disagree) * BIW]
+ ∑ [(LS * IMS_agree - LS * IMS_disagree) * IMIW]
+ ∑ [(LS * MS_agree - LS * MS_disagree) * MIW]

Where:

• CS: Conclusion Score
• LS is the Linkage Score, representing the strength of the connection between an argument and the conclusion it supports.
• n represents the number of steps an argument is removed from an idea. For instance, a direct reason to agree or disagree is one step removed, whereas a reason to agree with a reason to agree is two steps removed.
• RS, ES, IS, BS, IMS, and MS are scores associated with reasons, evidence, investments, books, images, and movies respectively that support or counter the belief. Each score is associated with a weighting factor (RIW, EIW, IIW, BIW, IMIW, and MIW) to signify its importance.

In this equation, each element (reason, evidence, investment, etc.) is first multiplied by its respective Linkage Score (LS) to represent the strength of the association with the conclusion, and then it contributes to the overall conclusion score (CS) in proportion to its importance weight (RIW, EIW, IIW, etc.). The score for each type is calculated as the difference between the scores for supporting and opposing elements.

Assistance Needed!
I'm seeking feedback on the clarity and feasibility of this concept. If there are any areas of confusion, or if the mathematical notation could be improved, I'd greatly appreciate suggestions.

Assumptions:
For instance, consider the belief that the leaders of Nazi Germany were evil. This belief is bolstered by many arguments, yet it can also serve as an argument itself, supporting other conclusions such as the idea that it was justifiable for the US to join WWII.

· Numerator: The numerator is obtained by subtracting the count of unique reasons to disagree from the count of unique reasons to agree. Consequently, if the "valid" reasons to agree are fewer, the numerator will be negative.

· Denominator: The denominator comprises the total count of reasons, both for and against. This computation normalizes the equation, rendering the conclusion score (CS) as the overall percentage of agreeable reasons. Therefore, the conclusion score will fluctuate between -100% and 100% (or -1 and +1).

· Definitions:
- A: Represents unique arguments that agree with a conclusion.
- D: Represents unique arguments that disagree with a conclusion.
- L: Stands for Linkage Score, a number between zero and 1. This metric quantifies the strength with which an argument is purported to support a conclusion.

· Unique Arguments: Every belief would have a template that enables the proposal of a statement that articulates the same idea more effectively. This statement would become a new argument with its unique conclusion score. For instance, if the rephrased belief gets a similarity rating of 98%, then it would contribute just 2% of its score to the new conclusion.

· For n = 1: Arguments like A(1,1) and A(1,2) are the first and second reasons to agree, respectively. Each contributes one point to the conclusion score, with the contribution moderated by the L (linkage score) multiplier.

· For n = 2: Arguments such as A(2,1) and A(2,2) are the first and second reasons to agree, where n equals 2. These could either be reasons agreeing with a reason to agree or reasons disagreeing with a reason to disagree. Each of these contributes half a point to the conclusion score due to the equation's design. Modifying the equation could change these contributions to a quarter point each to the conclusion score. This contribution is crucial since weakening an assumption logically weakens all conclusions built upon it. This value of n could be iteratively updated for reasonable results or uniquely determined by each platform. Note that D(n,j) represents reasons to disagree, and they function similarly. Here, j instead of i is used to indicate their independence. As such, second-order reasons to disagree could include reasons disagreeing with reasons to agree or reasons agreeing with reasons to disagree.

· L = Linkage Score: Let's consider the conclusion, "It was good for us to join WWII." An argument submitted could be, "Nazis were doing bad things," to support the conclusion. If this belief already has a high score of, say, 99%, it could be granted a linkage score of 90% towards supporting the conclusion. As a result, it would contribute 0.495 points (0.99 X 0.5) to the conclusion score for the belief, "It was good for us to join WWII". Another belief submitted could be, "Nazis were committing wide-scale systematic genocide," supporting the conclusion. Given that not all countries that "do bad things" justify a war, this linkage score could potentially be higher, perhaps 98%.

Investment-Based Scoring:

M = Money invested in a belief
TM = Total Money invested in the forum
#B = Number of beliefs

The average amount of money invested in an idea is computed as TM / #B. The aim of this metric is to assign 1 point for an idea with an average investment, and 2 points for a belief with double the average investment.

This concept is predicated on the idea of users being able to purchase “stock” in a belief based on its idea score, with the expectation that the idea score would rise. Transaction fees would be set high enough to prevent financial losses and ensure that only those with sound judgment profit from this mechanism. Additionally, stocks would only be sold for ideas that are relatively stable.

Certified Logic Instructors

• NP: Represents the number of times a certified** logic instructor has validated or invalidated the logic of a reason to disagree. By summing "ns", we can account for instances where a logic professor disagrees with a specific belief.

In our context, a "certified" logic instructor is defined as someone possessing a ".edu" email address associated with the philosophy department of an accredited university. This stipulation helps ensure that the individuals evaluating the logic of arguments have a credible academic background in the field of philosophy.

Book References

• B: Denotes books that support or oppose the given conclusion.
• BS: Book Score - takes into account factors like the number of books sold, as well as reviews and ratings of the books.
• BLS: Book Link Score - It's possible to have a well-regarded book that doesn't necessarily support the proposed belief. Each argument suggesting that a book supports a belief becomes its own claim with its own book "linkage score" that is calculated according to the above formula.

Voting System

• UV/DV: Upvotes or Downvotes.
• #U: Number of Users.
  We'll use an overall upvote or downvote system, in addition to votes on specific attributes like logic, clarity, originality, verifiability, and accuracy, among others.

Additional Evidence Sources

Movies, songs, expert opinions, and other sources of evidence can also support or oppose different conclusions, similarly to books. For example, movies - often documentaries - could be evaluated based on scores from sites like Rotten Tomatoes. This data could be imported, along with formal logical arguments that a movie attempts to support or oppose a belief.

**Certification for logic instructors is assumed to be from a reputable institution or organization. The exact criteria for certification can be defined based on the requirements of the forum.

Link Score (L)

When users submit beliefs as reasons to support other beliefs, they may occasionally attempt to forge a link where one doesn't truly exist. For instance, someone might submit the belief "The grass is green" as a reason to support the conclusion "The NY Giants will win the Super Bowl". Although the belief that "the grass is green" might receive a high score for its general acceptance, the "Link Score" in this context would be near zero due to its irrelevance to the conclusion.

• As we refine this system, we might have to apply multiplication factors to some elements to ensure that they do not carry too much or too little weight in the overall scoring.

Enriching Mathematical Learning Through the Practical Application of Algorithms

Dear Esteemed Mathematics Educators,

I am reaching out to you today with an exciting proposition - a unique opportunity to engage your students in the application of mathematical principles in an unconventional and meaningful way. It involves a novel algorithm designed to evaluate and promote ideas based on the strength of the reasoning and evidence provided.

Here is the formula we're discussing:

Conclusion Score (CS) = ∑ [(LS * RS_agree - LS * RS_disagree) * RIW]
+ ∑ [(LS * ES_agree - LS * ES_disagree) * EIW]
+ ∑ [(LS * IS_agree - LS * IS_disagree) * IIW]
+ ∑ [(LS * BS_agree - LS * BS_disagree) * BIW]
+ ∑ [(LS * IMS_agree - LS * IMS_disagree) * IMIW]
+ ∑ [(LS * MS_agree - LS * MS_disagree) * MIW]

More detailed information about these variables can be found on our websites: https://github.com/myklob/ideastockexchange and https://www.groupintel.org/.

In an era where discourse is increasingly digitized, this algorithm operates within a web-based forum. It allows users to submit reasons to agree or disagree with a belief, and encourages further discussion by allowing additional reasoning to be submitted for these primary arguments. The algorithm integrates these layers of discourse, forming an assessment of the belief's validity by counting and comparing reasons to agree and reasons to disagree.

Why introduce this into your mathematics curriculum?

1. Innovation: This algorithm provides a unique application of mathematical principles in an area traditionally untouched by such methods - the evaluation and promotion of ideas.

2. Engagement: By combining mathematics with discourse, debate, and real-world application, students can experience the practical and impactful side of their mathematical studies.

3. Idealism: This project aligns well with the idealistic nature of young minds. It enables students to contribute positively to global conversations, fostering a deeper connection to their learning.

4. Potential Impact: Just as Google's PageRank algorithm revolutionized the internet by ranking web pages based on their inbound links, our algorithm seeks to enhance discourse by assessing and promoting good ideas. This creates an informed and critical thinking internet community.

5. Towards a Smarter World: The development and use of such algorithms can contribute to a more informed, critical and intelligent world.

I encourage you to review this proposal and consider the immense potential it holds for enriching your curriculum and inspiring your students. I am eager to answer any questions or provide further information at your convenience.

Thank you for your time and consideration.

Best regards,
Mike

An open letter to Math teachers

I am writing you to ask for your assistance in promoting "good idea promoting algorithms" such as the following:

The above formula would work in an environment were you were able to submit reasons to agree or disagree with a belief, and then you could submit reasons to agree or disagree with those arguments. With this format it place you could count the reasons to agree and subtract the number of reasons to disagree, and then you could integrate the series of reasons to agree with reasons to agree.

You should use this equation because:

1. It is unique. I have never seen someone use an algorithm in an attempt to promote good ideas. Math can become more interesting when kids see the variety of ways it can be applied. 
2. Kids are idealistic, and often want to improve the world. Challenging them to try to come up with a good idea promoting algorithm can use this energy, to learn math.
3. This simple that counts the reasons to agree with a conclusion, could change the wold, similar to how Google's web-link counting algorithm changed the world. When lots of people link to a website, Google assumes that website is a good one. Then when that good website links to another website, Google assumes the 2nd website is a good one. Similarly when you submit good reasons to support an argument, a smart web forum would also give points to the conclusions that are built on that assumption. 
4. The more people make good idea promoting algorithms, the less stupid world we will live in.

Optimal Algorithm for Online Forums Utilizing Relational Databases for Debate

In an online forum that utilizes a relational database to track arguments either supporting or countering conclusions, and allows users to submit their beliefs as reasons to support other beliefs, the deployment of the following algorithm can prove highly advantageous:




Or with math:

The equation for the idea score can be represented as:

Basic Algorithm:

Conclusion Score (CS) is a weighted sum of different types of scores, each calculated as the difference between supporting and opposing elements for the given conclusion. It is represented as:

Conclusion Score (CS) = ∑ [(LS * RS_agree - LS * RS_disagree) * RIW]
+ ∑ [(LS * ES_agree - LS * ES_disagree) * EIW]
+ ∑ [(LS * IS_agree - LS * IS_disagree) * IIW]
+ ∑ [(LS * BS_agree - LS * BS_disagree) * BIW]
+ ∑ [(LS * IMS_agree - LS * IMS_disagree) * IMIW]
+ ∑ [(LS * MS_agree - LS * MS_disagree) * MIW]

Where:

• CS: Conclusion Score
• LS is the Linkage Score, representing the strength of the connection between an argument and the conclusion it supports.
• n represents the number of steps an argument is removed from an idea. For instance, a direct reason to agree or disagree is one step removed, whereas a reason to agree with a reason to agree is two steps removed.
• RS, ES, IS, BS, IMS, and MS are scores associated with reasons, evidence, investments, books, images, and movies respectively that support or counter the belief. Each score is associated with a weighting factor (RIW, EIW, IIW, BIW, IMIW, and MIW) to signify its importance.

The idea score is calculated by subtracting the sum of the argument scores multiplied by their respective linkage scores for the reasons to disagree from the sum of the argument scores multiplied by their respective linkage scores for the reasons to agree. This equation takes into account the relative strength and linkage of each argument in determining the overall idea score.

The equation for the linkage score can be represented as:

The linkage score is calculated by subtracting the sum of the sub argument scores that disagree from the sum of the sub argument scores that agree, and then dividing it by the total number of arguments. This value is then multiplied by 100% to express the result as a percentage. The linkage score represents the percentage of weighted scores that agree with the belief, indicating the strength of the agreement among the sub arguments in relation to the total number of arguments.

Unique Score (US) = [(Sum of scores agreeing that two statements are unique) - (Sum of scores disagreeing that two statements are unique)] / (Total argument scores) * 100

This score evaluates the uniqueness of two statements, normalizing it by the total argument scores. The score ranges from -100 to +100, where -100 indicates full agreement that two statements are not unique (or identical), and +100 indicates full agreement that two statements are indeed unique.

Math Question

I have a math equation I want to express correctly, but I have been out of college for 10 years and I’m a little rusty.

This is my attempt, but I’m not sure I have the series written correctly:

• n = number of steps an argument is removed from an idea, where a reason to agree is one step removed, but a reason to agree with a reason to agree is two steps. 
• A₁ = Number of reasons to agree (Count as 1 point each, towards the idea)
• D₁  = Number of reasons to disagree (Count as 1 point each, towards the idea)
• A₂ = Number of reasons to agree with reasons to agree or disagree with reasons to disagree (Count as 1/2 point each, towards the idea)
• D₂  = Number of reasons to disagree with reasons to agree or agree with reason to disagree (Count as 1/2 point each, towards the idea)
• and so on

I’m not sure I have enough summation symbols.  If I define A sub 1 as “Number of” can I leave out the extra summation symbols shown in this equation:

Other Factors: Additional Evidence such as Movies, Songs, Expert Opinions

Similar to books, various forms of media like movies (particularly documentaries), songs, or expert opinions can offer support or opposition to different perspectives. For instance, the website Rotten Tomatoes offers scores for movies which can be an indicator of the general consensus about the argument or message a film is putting forward. This data could be integrated into the evaluation of a belief or argument, along with any formal logical arguments presented within the media content.

The Link Score (L): When beliefs are submitted as reasons to support other beliefs, there's a risk of irrelevant arguments being included. For example, someone might claim that the belief "the grass is green" is a reason to believe "the New York Giants will win the Super Bowl." Although the belief that "the grass is green" might have a high agreement score, the relevance or "Link Score" will be close to zero due to the lack of a logical connection.

As this process is refined, certain multiplication factors may need to be applied to avoid giving too much or too little weight to certain factors.

** Credibility can often be gauged by looking at the source of information. For instance, those with a ".edu" email address from the philosophy department of an accredited university can be considered reliable, knowledgeable sources.

• Logical Arguments:
• Multidimensionality of Knowledge: Knowledge and perspectives can come from various sources, not limited to academic texts and discussions. Movies, songs, and expert opinions can provide rich and varied insights, supplementing our understanding.
• Supporting Evidence (data, studies):
• Numerous studies have demonstrated the educational potential of films and music (Marsh, Jackie. "Popular culture in the literacy curriculum: a 'Bourdieuan' perspective." Reading literacy and language (2003): 96-103.)
• Supporting Books:
• "Film as Philosophy: Essays on Cinema After Wittgenstein and Cavell" by Rupert Read and Jerry Goodenough: This book demonstrates the philosophical potential of films.
• "The Rest Is Noise: Listening to the Twentieth Century" by Alex Ross: It highlights the historical and cultural insights that can be drawn from music

Other Factors: Stuff, like movies, songs, experts, etc that agaree or disagree

Similar to how I say books can support or oppose different conclusions, movies (often documentaries) can support or oppose different conclusions. Rotten tomatoes gives scores to movies. All of this data could be imported, as well as the formal logical arguments that a movie actually attempts to support or oppose a belief.

L = Link score. When we submit beliefs as reasons to support other beliefs, and give higher scores to conclusions that have more reasons to agree with them, people will try to submit beliefs that don’t really support the conclusion. For instance someone might post the belief that the grass is green as a reason to believe the NY Giants will win the super bowl. The beliefs that the grass is green will receive a high score, but the “Link Score” as will be close to zero.

* As we work this out we may have to apply multiplication factors to not give too much or too little weight to a factor.

** Who has a “.edu” e-mail address from the philosophy department of an accredited university

Other Factors: Up/Down Votes

I think if we tracked the number of up votes and compared it to the number of down votes it might tell us a little about the quality of an argument, or at least its perceived quality.

I think the more information the better. This is the best equation I can come up with for adding points to a belief based on the number of up or down votes. I would love your feedback.

Below is an explanation of each term.

Up/Down Votes

• UV/DV = Up or Down Vote
• #U = Number of Users
• We will have overall up or down votes. We will also have votes on specific attributes like: logic, clarity, originality, verifiability, accuracy, etc.

Other Factors: Books that agree or Disagree

I believe that tracking the number of books suggested as reasons to agree or disagree with a conclusion could help develop algorithms that promote beliefs that have been thoroughly examined and supported.

Here's the best equation I've come up with for adding points to a belief based on the number and quality of books suggested as reasons to support or disagree with a conclusion:

Points = Σ(BS * BLS)

I'd appreciate your feedback on this approach and its potential effectiveness in promoting well-examined ideas.

Below is an explanation of each term:

B = Books that have been said to support or oppose the given conclusion

BS = Book Score, which can take into account the number of books sold, scores given by book reviewers, etc.

BLS = Book Link Score, which evaluates how well a book supports the proposed belief. Each argument that a book supports a belief becomes its own argument, and the book's "linkage score" is assigned points based on the equation provided above.

Other Factors: Incorporating Input from Logic Professors

I once took a course in logic taught by a professor of philosophy, a discipline in which formal logic often plays a crucial role.

My proposal involves quantifying the input of logic professors who "authenticate" the logic of an argument, juxtaposed against those who "contend" with the logic of the same argument. Such data could potentially bolster the credibility of ideas that have been meticulously scrutinized and validated.

Consider this modified equation, using a ratio to add or subtract points from a belief based on the input of logic professors:

Ratio = Number of times a certified logic instructor has authenticated the logic of a given argument (LPV) / Number of times a certified logic instructor has contested the logic of a given argument (LPC).

Using this ratio, if a logic professor opposes a reason that underpins your conclusion, the overall score would decrease proportionately. This is because the action of contesting is twice removed from directly affirming the belief, which is reflected in the ratio.

It's important to note that these equations would be adjusted and fine-tuned over time to improve the site's user engagement and overall performance. Our goal is to create a system that is flexible, responsive, and continually improving based on user interaction and feedback. Your thoughts and suggestions on this proposed approach would be greatly appreciated.


a) Fundamental Beliefs or Principles one must reject to also reject this belief:

• Rejection of Expertise: To disregard the idea of using evaluations from philosophy professors who have taught formal logic means rejecting the concept that individuals who have studied and taught critical thinking and formal logic possess a special skill set that can be used to assess the validity of arguments effectively.
• Rejection of Academic Knowledge: This also entails the rejection of the principle that academia, specifically in the field of philosophy and formal logic, contributes significantly to understanding and assessing arguments.
• Rejection of Objective Assessment: This further implies rejecting the idea that an argument's validity can be objectively analyzed based on established principles of formal logic.

b) Alternate Expressions:#LogicCheckedByAcademics

• #FormalLogicValidation
• "Endorsed by Philosophy Educators"

c) Objective Criteria to Measure the Strength of this Belief:

1. Number of Philosophy Professors who have taught Formal Logic that endorse the argument.
2. Consistency of their evaluation with established principles of formal logic.
3. The acceptance and application of their assessments in resolving disagreements or strengthening arguments.

d) Shared Interests between Those Who Agree/Disagree:

• Both sides likely value logical consistency and sound arguments.
• Both would probably appreciate a fair and objective assessment process.
• Both parties likely want the discussion or debate to contribute to truth and understanding, not merely winning an argument.

e) Key Opposing Interests between Those Who Agree/Disagree (that must be addressed for mutual understanding):

• Those who agree might feel that input from Philosophy Professors who have taught Formal Logic adds credibility and objectivity to the discussion.
• Those who disagree might fear this approach overly privileges academic knowledge, potentially excluding valuable perspectives from non-academics or individuals with practical, rather than formal, understanding of logic.
• For constructive dialogue, it is necessary to acknowledge the value of expert input while ensuring that all meaningful and insightful contributions are given due consideration.

f) Solutions:

• Create a balanced system where validations from philosophy professors who have taught formal logic are one of many factors considered in an argument's strength.
• Incorporate input from a diverse range of experts, not just philosophy academics experienced in formal logic.
• Implement a system that allows users to challenge or question the validations from these philosophy professors, fostering an open dialogue.

1. Logical Arguments:
1. Expertise Principle: Philosophy professors who have taught formal logic have acquired expert knowledge, making them well-suited to evaluate logical coherence in arguments.
2. Supporting Evidence (data, studies):
1. Studies on expertise suggest that experts, due to their training and experience, have deeper knowledge and insights in their areas of specialization (Ericsson, K. A., & Lehmann, A. C. (1996). Expert and exceptional performance: evidence of maximal adaptation to task constraints. Annual review of psychology, 47(1), 273-305).
3. Supporting Books:
1. "Thinking Fast and Slow" by Daniel Kahneman: This book, while not directly related to philosophy professors, discusses the differences between expert thinking and intuitive thinking.
4. Supporting Videos (movies, YouTube, TikTok):
1. "Crash Course Philosophy" on YouTube: A video series that provides an introduction to philosophy and logical reasoning.
5. Supporting Organizations and their Websites:
1. The American Philosophical Association (apaonline.org): An organization supporting the work of philosophers and the value of their expertise.
6. Supporting Podcasts:
1. "Philosophy Bites" is a podcast that showcases the insights of contemporary philosophers on a wide range of topics.
7. Unbiased Experts:
1. Professors of Philosophy who have taught formal logic, as their training ideally positions them to be impartial arbiters of logical consistency.
8. Benefits of Belief Acceptance (ranked by Maslow categories):
1. Psychological Needs: Encourages intellectual growth and cognitive satisfaction through engaging with logically sound arguments.
2. Belonging and Love Needs: Facilitates fair and meaningful dialogue, promoting a sense of community.
3. Esteem Needs: Upholds the value of academic knowledge and expertise, contributing to societal respect for intellectual pursuits.
4. Self-Actualization: Supports the pursuit of truth and understanding, key aspects of personal and societal development.