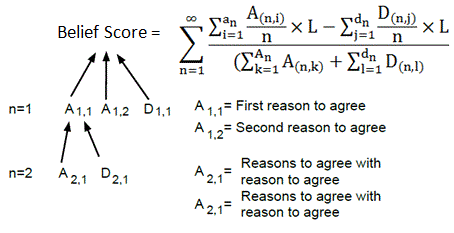Scoring Beliefs and Conclusions: An Algorithmic Approach for an Online Forum
This online forum employs a relational database to catalog reasons supporting or opposing various conclusions. It allows users to submit a belief as evidence to back another belief (Refer to Figure #1). According to Equation #1, a conclusion receives a score derived from the scores of its underpinning assumptions. Similarly, assumption scores are calculated based on their corresponding assumptions, until we reach verifiable data. Basic Algorithm: Conclusion Score (CS) is a weighted sum of different types of scores, each calculated as the difference between supporting and opposing elements for the given conclusion. It is represented as: Conclusion Score (CS) = ∑ [(LS * RS_agree - LS * RS_disagree) * RIW] + ∑ [(LS * ES_agree - LS * ES_disagree) * EIW] + ∑ [(LS * IS_agree - LS * IS_disagree) * IIW] + ∑ [(LS * BS_agree - LS * BS_disagree) * BIW] + ∑ [(LS * IMS_agree - LS * IMS_disagree) * IMIW] + ∑ [(LS * MS_agree - LS * MS_disagree) * MIW] Where: CS: Conclusion Score LS is the Linkage Sco...